My R-blog

A place to share interesting things about statistics, shape models and programming

  • GitHub projects
  • RSS feed

    • © 2024. All rights reserved.

    Use statismo models for elastic mesh registration in R

    14 Aug 2014

    I finally found some time to properly implement statismo models into the surface matching functions AmbergRegister and gaussMatch from my package mesheR.

    Here is an example how to do this:

    CAVEAT:

    You need to install latest version from master branch of mesheR, RvtkStatismo and Morpho !! 
    require(RvtkStatismo)
require(Rvcg)
require(Morpho)
require(mesheR)
require(rgl)
data(humface)
data(dummyhead)


### first create a model based on the reference
mymod <- statismoModelFromRepresenter(dummyhead.mesh,kernel = list(c(50,50),c(20,20),c(10,20),c(5,20)),ncomp = 100)## combine some Gaussian kernels

##now create an object of class BayesDeform

Bayes <- createBayes(mymod,sdmax=c(rep(3,5),ptValueNoise = 2))# this means that the first 5 elastic iterations are restricted to be within 3 standard deviations of our model and we provide some point noise for the landmarks
## setup parameters for AmbergRegister
params <- list(iterations=10)
params <- append(params, list(
        # then let it increase from 0.2 to 0.6
        lambda=seq(from = 0.2,to=0.6,length.out = params$iterations),
        # treat \code{k} similar as \code{lambda}
        k=seq(from = 1,to=params$iterations,by=1),
        useiter=FALSE # iteratively deform dummyhead onto humface
        ))

## setup parameters for some additional rigid wiggling (ICP)

rigid <- list(iterations=60,subsample=200,rhotol=pi/2,uprange=0.3)#here we specify an overlap between reference and target of 30% 

## run the matching
map <- AmbergRegister(dummyhead.mesh, humface, lm1=dummyhead.lm, lm2=humface.lm, iterations=params$iterations,k=params$k, lambda=params$lambda, useiter=params$useiter,rigid=rigid,Bayes=Bayes)

## show the results
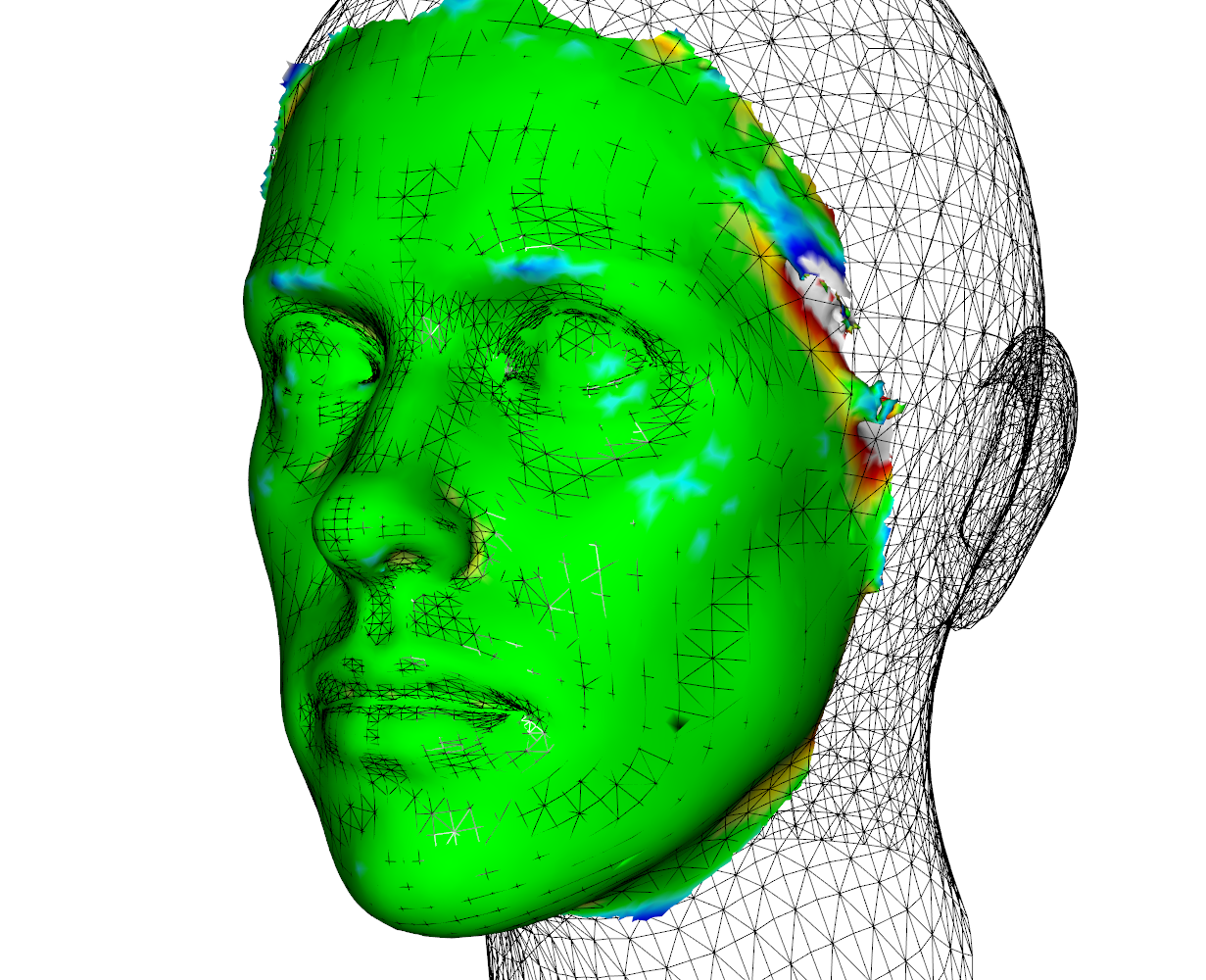
meshDist(humface,map$mesh,tol=0.5,from=-3,to=3)## create heatmap with distances (figure 1)
wire3d(map$mesh)##this is our matched mesh # figure 2

## check if landmarks are in a reasonable position
spheres3d(map$lm1,col=2)##mapped landmarks
spheres3d(humface.lm)##original landmarks

## Additionally, we can look at that shape within the model space that is closest to our surface (figure 3)
modelsurf <- PredictSample(mymod,map$mesh,T)
wire3d(modelsurf,col=2)
## we can see that the shape of the cheeks is not represented well by the model but the overall shape is

    And here is an example with Marcel’s Femur surfaces:

    
require(RvtkStatismo)
require(Rvcg)
require(Morpho)
require(mesheR)
require(rgl)

download.file(url="https://github.com/marcelluethi/statismo-shaperegistration/raw/master/data/VSD001_femur.vtk","./VSD001_femur.vtk",method = "w")
download.file(url="https://github.com/marcelluethi/statismo-shaperegistration/raw/master/data/VSD002_femur.vtk","./VSD002_femur.vtk",method = "w")
download.file(url="https://github.com/marcelluethi/statismo-shaperegistration/raw/master/data/VSD001-lm.csv","./VSD001-lm.csv",method = "w")
download.file(url="https://github.com/marcelluethi/statismo-shaperegistration/raw/master/data/VSD002-lm.csv","./VSD002-lm.csv",method = "w")

ref <- read.vtk("VSD001_femur.vtk")
tar <- read.vtk("VSD002_femur.vtk")

ref.lm <- as.matrix(read.csv("VSD001-lm.csv",row.names=1))
tar.lm <- as.matrix(read.csv("VSD002-lm.csv",row.names=1))
mymod <- statismoModelFromRepresenter(ref,kernel=list(c(50,50),c(10,10)),ncomp = 100)

Bayes <- createBayes(mymod,sdmax = rep(6,10))##restrict first 10 iterations to model

## setup similarity and affine icps
similarity = list(iterations=10,rhotol=pi/2)
affine = list(iterations=10,rhotol=pi/2)

matchGP <- gaussMatch(ref,tar,lm1 = ref.lm,lm2=tar.lm,sigma = 30,gamma=4,smooth=1,smoothit = 10,smoothtype = "t",iterations = 15,toldist = 50,angtol = pi/2,Bayes=Bayes,similarity = similarity,affine = affine)

## view displacement field (figure below):
require(Morpho)
deformGrid3d(matchGP,ref,size=0.1,type="p")

    EDIT:

    I just realized, that we actually do not need smoothing (to prevent mesh-folding) if we use statistical models because the model carries us pretty close to a valid target shape:

    
matchGPNoSmooth <- gaussMatch(ref,tar,lm1 = ref.lm,lm2=tar.lm,sigma = 30,gamma=4,smooth=NULL,iterations = 15,toldist = 50,angtol = pi/2,Bayes=Bayes,similarity = similarity,affine = affine)

    Now, when looking at the deformed reference, we can still see the mesh structure produced by marching cubes (so I assume):

    Related Posts